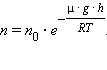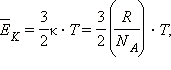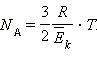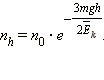|
Опыт Перрена: броуновское движение
|
 |
 |
|
Перрен Жан Батист
|
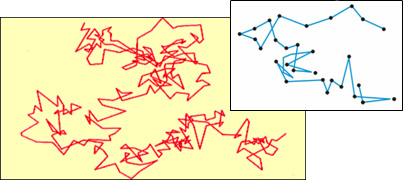
В 1827 г. английский ботаник Роберт Броун впервые использовал для проведения своих научных экспериментов ахроматический объектив. Мелкие споры цветочной пыльцы, плавающие в капле воды, совершали хаотические импульсные движения. Движение было непрерывным и ни на миг не прекращалось. Вода в капле была неподвижна, так что объяснить движение частиц с завихрениями течений в капле не удалось. Кроме цветочной пыльцы, ученый исследовал пыль и минеральные порошки, характеристики движения были сходны для различных мелких объектов и не зависили от их химического состава. Обнаруженное ученым движение взвешенных частиц стало называться в его честь броуновским движением (рис. 1).
 |
|
Рис. 1. Траектории движения броуновских частиц
|
Первоначально ученые не проявляли особого интереса к открытому Броуном явлению. Тем более, не предпринималось
Во второй половине XIX века объяснение данного явление заинтересовало многих ученых. Началось его активное изучение. Выяснилось, что движение каждой частицы является непрерывным и не связано с движением окружающих частиц. Оказалось, что оно не зависит от яркости направленного на него света. При этом на скорость частиц влияет их масса. Мелкие частицы двигались быстрее, чем крупные.
В 1863 г. Людвиг Кристиан Винер, обобщив результаты всех ранее проведенных исследований, установил, что это броуновское движение вызвано вовсе не внешними воздействиями, а определяется только внутренними движениями, присущими самой жидкости. Оно обязано своим происхождением столкновениям броуновской частицы с молекулами жидкости. Винер впервые попытался измерить скорость перемещения броуновских частиц и ее зависимость от их размера.
Поразительно, но почти аналогичное объяснение в своей знаменитой поэме «О природе вещей» дал похожему явлению римский философ Тит Лукреций Кар
«Первоначала вещей сначала движутся сами,
Следом за ними тела из мельчайшего их сочетанья,
Близкие, как бы сказать, по силам к началам первичным,
Скрыто от них получая толчки, начинают стремиться,
Сами к движенью затем побуждая тела покрупнее.
Так, исходя от начал, движение мало-помалу
Наших касается чувств, и становится видимым также
Нам и в пылинках оно, что движутся в солнечном свете,
Хоть незаметны толчки, от которых оно происходит»
К сожалению, выводы Винера о природе броуновского движения не получили всеобщего признания. Существовали другие объяснения открытого Броуном движения. Так, например, Г. Квинке рассматривал броуновское движение как следствие температурных разностей в жидкости. Джевонс высказал предположение, что броуновское движение вызвано электрическими силами. Однако Дансер в 1870 г. доказал, что броуновское движение не является следствием действия электрических сил. Много позднее в 1892 г. английский физик и химик Уильям Рамзей тоже выступил против электрического объяснения движения броуновских частиц.
Исследования броуновского движения продолжались год за годом. В 1865 г. Джованни Кантони и Эль, исследуя препарат, заключенный между двумя стеклянными пластинками, установили, что характер броуновского движения не менялся в течение целого года. В 1867 г. Ф. М. Экснер еще раз экспериментально подтвердил, что интенсивность движения зависит от размеров частиц. Ему удалось обнаружить, что и световое, и тепловое воздействие тоже влияли на скорость их движения.
В 1870 г. бельгийские священники Э. Карбонелль и Д. Дельсо, также как и О. Винер, пришли к выводу, что броуновское движение вызвано столкновением молекул жидкости со взвешенными частицами. «При большой площади, – писали Дельсо и Э. Карбонелль, – удары молекул, являющиеся причиной давления, не вызывают никакого сотрясения подвешенного тела, потому что они в совокупности создают равномерное давление на тело во всех направлениях. Но если площадь недостаточна, чтобы скомпенсировать неравномерность, нужно учесть неравенство давлений и их непрерывное из менение от точки к точке. Закон больших чисел не сводит теперь эффект соударений к среднему равномерному давлению, их равнодействующая уже не будет равна нулю, а будет непрерывно изменять свое направление и свою величину».
Наиболее точные исследования броуновского движения провел французский физик Луи Жорж Гуи. Он установил, что интенсивность броуновского движения возрастает с уменьшением внутреннего трения жидкости, никак не зависит от интенсивности освещения и внешнего электромагнитного поля. Он также пришел к выводу, что броуновское движение вызвано влиянием теплового движения молекул. Л. Ж. Гуи оценил скорость броуновских частиц, она оказалась равной приблизительно одной стомиллионной молекулярной скорости.
К концу XIX в. многим ученым стало очевидно, что движение броуновских частиц вызвано беспорядочными ударами молекул среды. Но были и те, которые все же не соглашались с этой точкой зрения, так как не верили в существование молекул. Так, крупнейший французский
Как видно, мнения различных ученых относительно истинности молекулярных воззрений были прямо противоположными.
Несмотря на то, что в начале XX в. большинство ученых верно понимали молекулярную природу броуновского движения, все объяснения этого явления оставались чисто качественными. Количественной теории явления не существовало. Соответственно не было ясно, какие именно характеристики этого явления нужно измерить, чтобы убедиться в справедливости молекулярной теории строения вещества.
Как это ни удивительно, но кажущийся беспорядок этого движения и случайные перемещения броуновских частиц оказалось все же возможным описать математической формулой. Впервые строгое объяснение броуновского движения дал в 1904 польский физик Мариан Смолуховский
Эйнштейн, исходя из того, что броуновское движение является хаотическим, как и тепловое движение вызывающих его молекул, построил статистическую количественную теорию этого движения. На основании результатов своей работы он вычислил постоянную Авогадро, размеры броуновских частиц, вязкость жидкости и т. д.
Позднее ученый признался, что он вообще не знал о броуновском движении и «открыл» его чисто теоретическим путем: «Не зная, что наблюдения над «броуновским движением» давно известны, я открыл, что атомистическая теория приводит к существованию доступного наблюдению движения микроскопических взвешенных частиц».
В соответствии с теорией
|
где
Оказалось принципиально важным, что в эту формулу входит постоянная Авогадро, которую теперь можно было определить путем количественных измерений перемещения броуновской частицы.
В 1908 г. французский физик Жан Батист Перрен ставит эксперимент, результаты которого должны были стать прямым подтверждением статистической теории броуновского движения
Истинность этой теории Перрен проверил, исследуя распределение частиц эмульсии по высоте. В основу экспериментальной работы Перрена легли результаты исследования Л. Больцмана. В 1876 г. немецкий физик Людвиг Больцман
|
 |
|
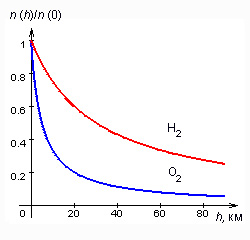
Рис. 2. Распределение молекул различных газов в воздухе в поле тяжести согласно закону Больцмана
|
Ж. Б. Перрен применил эту формулу для исследования распределения броуновских частиц с высотой. Он предположил, что систему из броуновских частиц можно рассматривать в качестве модели
Действительно, например, молекулы кислорода и азота в воздухе, двигаясь в среднем со скоростью примерно
|
|
|
Модель 1. Кинетическая модель идеального газа
|
|
|
|
Модель 2. Модель броуновского движения
|
Понимание принципиальной общности поведения молекул газа и броуновских частиц позволило Перрену применить ряд известных законов для газов и к описанию поведения броуновских частиц.
Итак, эксперимент, поставленный Перреном, был направлен на проверку полученных теоретическим путем математических закономерностей, которым подчиняется броуновское движение. В случае успеха получала подтверждение и молекулярная теория строения вещества
Для проверки статистической теории
Для наблюдений Перрен использовал изобретенный в 1902 г. ультрамикроскоп. Микроскоп этой конструкции позволял видеть мельчайшие частицы благодаря рассеянию на них света от мощного бокового осветителя.
Большого труда потребовала от экспериментатора подготовка эмульсии с частичками гуммигута – сгущенного сока некоторых тропических деревьев. Смолу Перрен растер в воде. Под микроскопом было видно, что в подкрашенной воде находится огромное число желтых шариков. Эти шарики отличались по величине, они представляли собой твердые образования, которые не слипались друг с другом при соударениях. Чтобы распределить шарики по размеру, Перрен помещал пробирки с эмульсией в центробежную машину. Машина приводилась во вращение. За несколько месяцев кропотливой работы Перрену удалось наконец получить порции эмульсии с одинаковыми по размеру зернами гуммигута
Одинаковые по размеру зернышки раствора должны были расположиться по предположению Перрена в соответствии с законом распределения числа частиц с высотой. Именно для исследования распределения частиц по высоте экспериментатор сделал в предметном стекле цилиндрическое углубление. Это углубление он заполнил эмульсией, затем закрыл сверху покровным стеклом. Для наблюдения эффекта Ж. Б. Перрен использовал микроскоп с малой глубиной изображения
|
|
|
|
Рис. 3. Метод наблюдения броуновских частиц в микроскоп в опыте Перрена
|
Свои исследования Перрен начал с проверки основной гипотезы статистической теории Эйнштейна. Вооружившись микроскопом и секундомером, он наблюдал и фиксировал в освещенной камере положения одной и той же частицы эмульсии через одинаковые промежутки времени.
Наблюдения показали, что беспорядочное движение броуновских частиц приводило к тому, что они перемещались в пространстве очень медленно. Частицы совершали многочисленные возвратные движения. В итоге сумма отрезков между первым и последним положениями частицы была намного больше прямого смещения частицы от первой точки до последней.
Перрен отмечал и потом зарисовывал в масштабе на разграфленном листе бумаги положение частиц через равные временные интервалы. Наблюдения проводились через каждые 30 с. Соединяя полученные точки прямыми, он получал замысловатые ломанные траектории.
Далее Перрен определил число частиц в разных по глубине расположения слоях эмульсии. Для этого он последовательно фокусировал микроскоп на отдельные слои взвеси. Выделение каждого последующего слоя осуществлялось через каждые 30 микрон. Таким образом, Перрен мог наблюдать число частиц, находящихся в очень тонком слое эмульсии. Частицы других слоев при этом не попадали в фокус микроскопа. Используя этот метод, ученый мог количественно определить изменение числа броуновских частиц с высотой.
Опираясь на результаты последнего эксперимента, Перрен смог определить значение числа Авогадро –
Способ расчета фундаментальной константы базировался на следующих рассуждениях.
Броуновские частицы, как и молекулы, находятся в беспорядочном движении. Соответственно, они подчиняются всем газовым законам. Из общих соображений можно показать, что средняя кинетическая энергия
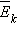 одной броуновской частицы равна средней кинетической энергии молекул при данной температуре
одной броуновской частицы равна средней кинетической энергии молекул при данной температуре
|
где
Из этой формулы можно выразить число Авогадро
|
Определив среднюю кинетическую энергию 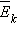 броуновской частицы при данной температуре, можно найти значение
броуновской частицы при данной температуре, можно найти значение 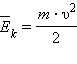 по массе частицы
по массе частицы 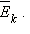 Тогда формула Больцмана приобретет вид:
Тогда формула Больцмана приобретет вид:
|
Зная массу частиц 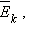 а затем и число Авогадро –
а затем и число Авогадро –
Очевидно, что для определения числа Авогадро необходимо найти массу шариков гуммигута. С той целью Перрен выпаривал каплю раствора гуммигута. Взвесив сухой остаток, он сосчитал количество зернышек, затем определил размеры и массу каждого из них.
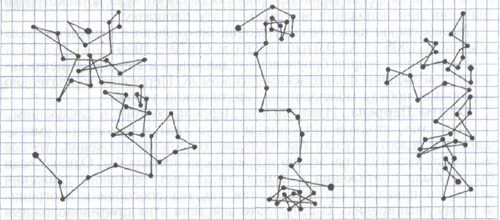
Наблюдая в освещенной камере через равные промежутки времени последовательные положения взвешенных в растворе глицерина частиц, Ж. Б. Перрен обнаружил, что они совершали непрерывное хаотическое движение (рис. 4). Ученый выполнил построение положений для ряда броуновских частиц на основании большого числа наблюдений (около 500). На рис. 4 представлена копия фотоснимка результатов его опыта.
 |
|
Рис. 4. Рисунки траекторий броуновских частиц из книги Ж. Перрена «Атомы», опубликованной в 1920 г. в Париже
|
Обработав полученные результаты, Перрен доказал, что средний квадрат перемещения броуновской частицы пропорционален времени ее движения :
|
|
Наблюдая в микроскоп расположение частиц гуммигута в слоях раствора, находившихся на разной высоте, Перрен заметил, что число частиц в жидкости убывало с высотой, причем очень быстро: через каждые 30 микрон их количество в слое сокращалось почти вдвое. На рис. 5 представлены изображения «населенности» различных слоев раствора броуновскими частицами. Видно, что в нижнем слое частиц много, а в верхнем мало.
|
|
|
|
Рис. 5. Распределение броуновских частиц в слоях на разной высоте
|
Это свидетельствовало как о справедливости полученного Л. Больцманом закона распределения молекул атмосферного воздуха в поле тяготения, так и о применимости этого закона к распределению числа броуновских частиц по высоте.
Перрен применил формулу закона распределения числа частиц с высотой для определения числа Авогадро –
В другой серии экспериментов, в которых измерялось среднеквадратичное смещение частиц в результате их броуновского движения, Перрен получил значение:
До опыта Ж. Б. Перрена
Было найдено значение числа Авогадро – одной из фундаментальных постоянных, определяющих строение нашего мира. Ее значение, полученное современными методами, равно:
|
|
Результаты опыта Перрена явились блестящим подтверждением теоретических выводов А. Эйнштейна. Этот факт произвел весьма сильное впечатление на научную общественность. Как написал через много лет американский физик А. Пайс «не перестаешь удивляться этому результату, полученному таким простым способом: достаточно приготовить взвесь шариков, размер которых велик по сравнению с размером простых молекул, взять секундомер и микроскоп, и можно определить постоянную Авогадро!».
После публикации результатов Ж. Б. Перрена бывший противник атомизма В. Оствальд признался, что «совпадение броуновского движения с требованиями кинетической гипотезы... дает теперь право самому осторожному ученому говорить об экспериментальном доказательстве атомистической теории материи. Таким образом, атомистическая теория возведена в ранг научной, прочно обоснованной теории». С ним соглашается французский математик и физик Анри Пуанкаре: «Блестящее определение числа атомов Перреном завершило триумф атомизма... Атом химиков стал теперь реальностью».
Опыты по исследованию броуновского движения продолжаются и до настоящего времени. Проведенный эксперимент по отслеживанию броуновского движения частицы с точностью до нанометров и микросекунд показал, что это движение имеет механизм, отличный от того, который описал А. Эйнштейн столетие назад. Эйнштейн полагал, что хаотическое движение частиц вызывается только случайными температурными колебаниями молекул окружающей жидкости. Сегодня ученые установили, что природа движения намного сложнее. Броуновское движение зависит от множества фундаментальных процессов внутри системы. Выяснилось, что хаотично движущаяся в своей среде частица может использоваться как своего рода «разведчик» в наномире. Исследователи уже научились получать информацию о системе, анализируя траектории движения в ней броуновских частиц. Для проведения такого эксперимента используется фотонный силовой микроскоп. С его помощью удается зарегистрировать с микросекундной частотой движения частицы и найти экспериментальное подтверждение ранее выдвинутым теориям. В результате таких экспериментов в классическую формулу броуновского движения были внесены исправления, позволяющие теперь адекватно описывать наномасштабные процессы .
Теория броуновского движения нашла широкое применение не только для описания случайного движения броуновской частицы в жидкости. Она оказалась применима и для решения широкого круга прикладных задач. Этой теории подчиняются случайные тепловые колебания высокоточных измерительных устройств (например, крутильных весов, гальванометров). Уравнения теории броуновского движения могут использоваться для анализа точности работы различных управляющих систем. С их помощью можно рассчитать случайные ошибки, которые возникают при управлении техническими устройствами, и выполнить оптимизацию параметров работы последних .


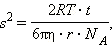
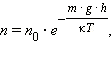 или
или